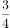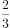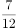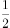试题要求
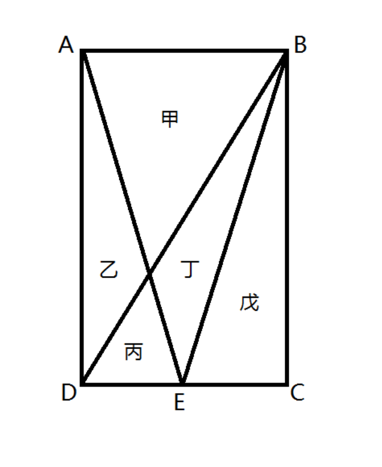
(单选题)一块种植花卉的矩形土地如图所示,AD边长是AB的2倍,E是CD的中点,甲、乙、丙、丁、戊区域分别种植白花、红花、黄花、紫花、白花。则种植白花的面积占矩形土地面积的:

答案解析
答案:C
解析:
方法一:设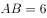 ,
,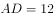 。由题意可得,三角形戊的面积
。由题意可得,三角形戊的面积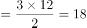 ;由AB和DE平行可知三角形甲和丙为相似三角形,已知
;由AB和DE平行可知三角形甲和丙为相似三角形,已知 ,所以三角形甲和丙的高之比也为
,所以三角形甲和丙的高之比也为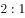 ,已知
,已知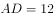 ,故三角形甲的高为
,故三角形甲的高为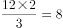 ,三角形甲的面积
,三角形甲的面积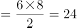 ;因为甲和戊种植白花,所以种植白花的面积共
;因为甲和戊种植白花,所以种植白花的面积共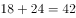 ,占矩形土地面积的
,占矩形土地面积的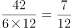 。
。
方法二:设丙的面积为1份,则根据 和
和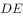 平行可知三角形甲和丙为相似三角形且
平行可知三角形甲和丙为相似三角形且 ,可知甲和丙的面积之比为
,可知甲和丙的面积之比为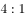 ,甲的面积为4份。分析比例关系可得乙+丙=丁+丙,故,乙和丁的面积相等,且均为丙的2倍,即面积为2份。再根据丁与丙构成的三角形与戊面积相等,可知戊的面积为
,甲的面积为4份。分析比例关系可得乙+丙=丁+丙,故,乙和丁的面积相等,且均为丙的2倍,即面积为2份。再根据丁与丙构成的三角形与戊面积相等,可知戊的面积为 。故白花面积为甲、戊面积之和,即
。故白花面积为甲、戊面积之和,即 ,总面积为
,总面积为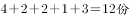 ,所以白花面积占比为
,所以白花面积占比为 。
。
故正确答案为C。
方法一:设
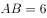 ,
,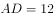 。由题意可得,三角形戊的面积
。由题意可得,三角形戊的面积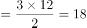 ;由AB和DE平行可知三角形甲和丙为相似三角形,已知
;由AB和DE平行可知三角形甲和丙为相似三角形,已知 ,所以三角形甲和丙的高之比也为
,所以三角形甲和丙的高之比也为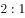 ,已知
,已知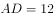 ,故三角形甲的高为
,故三角形甲的高为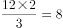 ,三角形甲的面积
,三角形甲的面积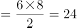 ;因为甲和戊种植白花,所以种植白花的面积共
;因为甲和戊种植白花,所以种植白花的面积共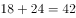 ,占矩形土地面积的
,占矩形土地面积的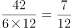 。
。
方法二:设丙的面积为1份,则根据
 和
和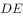 平行可知三角形甲和丙为相似三角形且
平行可知三角形甲和丙为相似三角形且 ,可知甲和丙的面积之比为
,可知甲和丙的面积之比为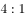 ,甲的面积为4份。分析比例关系可得乙+丙=丁+丙,故,乙和丁的面积相等,且均为丙的2倍,即面积为2份。再根据丁与丙构成的三角形与戊面积相等,可知戊的面积为
,甲的面积为4份。分析比例关系可得乙+丙=丁+丙,故,乙和丁的面积相等,且均为丙的2倍,即面积为2份。再根据丁与丙构成的三角形与戊面积相等,可知戊的面积为 。故白花面积为甲、戊面积之和,即
。故白花面积为甲、戊面积之和,即 ,总面积为
,总面积为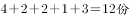 ,所以白花面积占比为
,所以白花面积占比为 。
。
故正确答案为C。
考点:几何问题
相似试题
- 1.(单选题)阳光下,电线杆的影子投射在墙面及地面上,其中墙面部分的高度为1米,地面部分的长度为7米。甲身高1.8米,同一时刻在地面形成的影子长0.9米。则该电线杆的高度为:
- 2.(单选题)科考队员在冰面上钻孔获取样本,测量不同空心之间的距离,获得的部分数据分别为1米、3米、6米、12米、24米、48米。问科考队员至少钻了多少个孔:
- 3.(单选题)某次军事演习中,一架无人机停在空中对三个地面目标点进行侦察。已知三个目标点在地面上的连线为直角三角形,两个点之间的最远距离为600米。问无人机与三个点同时保持500米距离时,其飞行高度为多少米?
- 4.(单选题)一个立方体随意翻动,每次翻动朝上一面的颜色与翻动前都不同,那么这个立方体的颜色至少有几种:
- 5.(单选题)为了浇灌一个半径为10米的花坛,园艺师要在花坛里布置若干个旋转喷头,但库房里只有浇灌半径为5米的喷头,问花坛里至少要布置几个这样的喷头才能保证每个角落都能浇灌到: