试题要求
（单选题）某次军事演习中，一架无人机停在空中对三个地面目标点进行侦察。已知三个目标点在地面上的连线为直角三角形，两个点之间的最远距离为600米。问无人机与三个点同时保持500米距离时，其飞行高度为多少米？
答案解析
答案：D
解析：
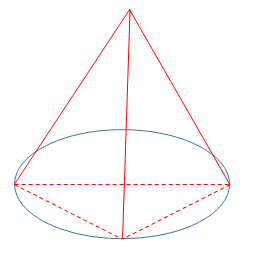
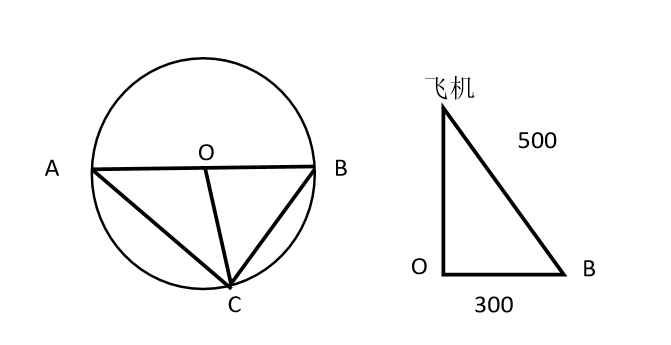
因飞机到三个目标点构成的平面的距离为定值，又因飞机与三个点保持相同距离，则飞机在该平面的投影点与三个目标点的距离相等，如图所示，飞机在该平面的投影为O点，A、B、C分别表示三个目标点，则以O点为圆心，AB（即相距最远的点）为直径画圆，其中C点在圆弧上。因为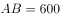
，所以
，而飞机到B点的距离为500米，故根据勾股定理，飞机与地面相距的距离为
米。
故正确答案为D。
因飞机到三个目标点构成的平面的距离为定值，又因飞机与三个点保持相同距离，则飞机在该平面的投影点与三个目标点的距离相等，如图所示，飞机在该平面的投影为O点，A、B、C分别表示三个目标点，则以O点为圆心，AB（即相距最远的点）为直径画圆，其中C点在圆弧上。因为
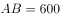，所以，而飞机到B点的距离为500米，故根据勾股定理，飞机与地面相距的距离为米。
故正确答案为D。
考点：几何问题
相似试题
- 1.（单选题）将一块长24厘米、宽16厘米的木板分割成一个正方形和两个相同的圆形，其余部分弃去不用。在弃去不用的部分面积最小的情况下，圆的半径为多少厘米？
- 2.（单选题）若干个相同的立方体摆在一起，前、后、左、右的视图都是，问这堆立方体最少有多少个？
- 3.（单选题）一艘非法渔船作业时发现其正右方有海上执法船，于是沿下图所示方向左转后，立即以15节（）的速度逃跑，同时执法船沿某一直线方向匀速追赶，并正好在某一点追上。已知渔船在被追上前逃跑的距离刚好与其发现执法船时
- 4.（单选题）草地上插了若干根旗杆，已知旗杆的高度在1至5米之间，且任意两根旗杆的距离都不超过它们高度差的10倍。如果用一根绳子将所有旗杆都围进去，在不知旗杆数量和位置的情况下，最少需要准备多少米长的绳子：
- 5.（单选题）科考队员在冰面上钻孔获取样本，测量不同空心之间的距离，获得的部分数据分别为1米、3米、6米、12米、24米、48米。问科考队员至少钻了多少个孔：