试题要求
（单选题）某次军事演习中，一架无人机停在空中对三个地面目标点进行侦察。已知三个目标点在地面上的连线为直角三角形，两个点之间的最远距离为600米。问无人机与三个点同时保持500米距离时，其飞行高度为多少米？
答案解析
答案：D
解析：
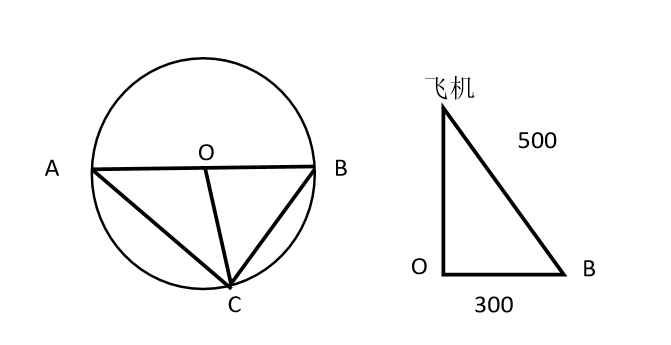
因飞机到三个目标点构成的平面的距离为定值，又因飞机与三个点保持相同距离，则飞机在该平面的投影点与三个目标点的距离相等，如图所示，飞机在该平面的投影为O点，A、B、C分别表示三个目标点，则以O点为圆心，AB（即相距最远的点）为直径画圆，其中C点在圆弧上。因为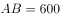
，所以
，而飞机到B点的距离为500米，故根据勾股定理，飞机与地面相距的距离为
米。
故正确答案为D。
因飞机到三个目标点构成的平面的距离为定值，又因飞机与三个点保持相同距离，则飞机在该平面的投影点与三个目标点的距离相等，如图所示，飞机在该平面的投影为O点，A、B、C分别表示三个目标点，则以O点为圆心，AB（即相距最远的点）为直径画圆，其中C点在圆弧上。因为
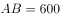，所以，而飞机到B点的距离为500米，故根据勾股定理，飞机与地面相距的距离为米。
故正确答案为D。
考点：几何问题
相似试题
- 1.（单选题）连接正方体每个面的中心构成一个正八面体（如下图所示）。已知正方体的边长为6厘米，则正八面体的体积为多少立方厘米：
- 2.（单选题）现要在一块长25公里、宽8公里的长方形区域内设置哨塔，每个哨塔的监视半径为5公里。如果要求整个区域内的每个角落都能被监视到，则至少需要设置多少个哨塔：
- 3.（单选题）若干个相同的立方体摆在一起，前、后、左、右的视图都是，问这堆立方体最少有多少个？
- 4.（单选题）将一块长24厘米、宽16厘米的木板分割成一个正方形和两个相同的圆形，其余部分弃去不用。在弃去不用的部分面积最小的情况下，圆的半径为多少厘米？
- 5.（单选题）将一块长24厘米、宽16厘米的木板分割成一个正方形和两个相同的圆形，其余部分弃去不用。在弃去不用的部分面积最小的情况下，圆的半径为多少厘米？