试题要求
（单选题）现要在一块长25公里、宽8公里的长方形区域内设置哨塔，每个哨塔的监视半径为5公里。如果要求整个区域内的每个角落都能被监视到，则至少需要设置多少个哨塔：
答案解析
答案：C
解析：
如下图所示：
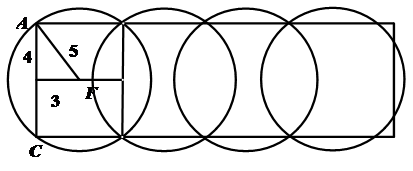
根据直角三角形勾股定理
，则每个圆形可覆盖一个宽为
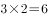公里的长方形。要达到完全覆盖，故需要
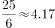个，至少5个。
故正确答案为C。
如下图所示：
根据直角三角形勾股定理
，则每个圆形可覆盖一个宽为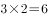公里的长方形。要达到完全覆盖，故需要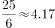个，至少5个。
故正确答案为C。
考点：几何问题
相似试题
- 1.（单选题）将一个棱长为整数的正方体零件切掉一个角，截面是面积为的三角形，问其棱长最小为多少？
- 2.（单选题）现要在一块长25公里、宽8公里的长方形区域内设置哨塔，每个哨塔的监视半径为5公里。如果要求整个区域内的每个角落都能被监视到，则至少需要设置多少个哨塔：
- 3.（单选题）阳光下，电线杆的影子投射在墙面及地面上，其中墙面部分的高度为1米，地面部分的长度为7米。甲身高1.8米，同一时刻在地面形成的影子长0.9米。则该电线杆的高度为：
- 4.（单选题）将一个8厘米×8厘米×1厘米的白色长方体木块的外表面涂上黑色颜料，然后将其切成64个棱长1厘米的小正方体，再用这些小正方体堆成棱长4厘米的大正方体，且使黑色的面向外露的面积要尽量大，问大正方体的表面上
- 5.（单选题）草地上插了若干根旗杆，已知旗杆的高度在1至5米之间，且任意两根旗杆的距离都不超过它们高度差的10倍。如果用一根绳子将所有旗杆都围进去，在不知旗杆数量和位置的情况下，最少需要准备多少米长的绳子：