试题要求
(单选题)将一个棱长为整数的正方体零件切掉一个角,截面是面积为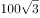 的三角形,问其棱长最小为多少?
的三角形,问其棱长最小为多少?
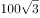 的三角形,问其棱长最小为多少?
的三角形,问其棱长最小为多少?答案解析
答案:A
解析:
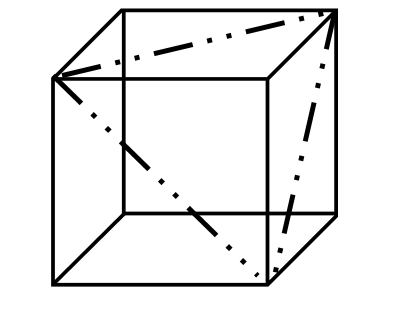
如图所示,在截面面积固定不变的情况下,要让棱长尽量小,则截面尽量大。正方体中满足切掉一个角的最大的截面如虚线所示,其面积是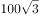 。由于三条虚线都是正方体的面对角线,彼此相等,所以是正三角形。
。由于三条虚线都是正方体的面对角线,彼此相等,所以是正三角形。
假设该正三角形边长为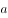 ,则正三角形面积为:
,则正三角形面积为: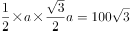 ,解得
,解得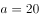 ,则正方体其中一个面的对角线长度为20,正方体边长为
,则正方体其中一个面的对角线长度为20,正方体边长为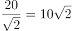 ,已知棱长为整数,则其最小值为15。
,已知棱长为整数,则其最小值为15。
注意:有的截面积更大的切法,不满足切下来的必须是一个角的要求,故错误。
故正确答案为A。

如图所示,在截面面积固定不变的情况下,要让棱长尽量小,则截面尽量大。正方体中满足切掉一个角的最大的截面如虚线所示,其面积是
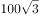 。由于三条虚线都是正方体的面对角线,彼此相等,所以是正三角形。
。由于三条虚线都是正方体的面对角线,彼此相等,所以是正三角形。
假设该正三角形边长为
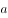 ,则正三角形面积为:
,则正三角形面积为: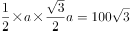 ,解得
,解得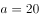 ,则正方体其中一个面的对角线长度为20,正方体边长为
,则正方体其中一个面的对角线长度为20,正方体边长为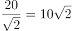 ,已知棱长为整数,则其最小值为15。
,已知棱长为整数,则其最小值为15。
注意:有的截面积更大的切法,不满足切下来的必须是一个角的要求,故错误。
故正确答案为A。
考点:几何问题
相似试题
- 1.(单选题)将一块长24厘米、宽16厘米的木板分割成一个正方形和两个相同的圆形,其余部分弃去不用。在弃去不用的部分面积最小的情况下,圆的半径为多少厘米?
- 2.(单选题)某次军事演习中,一架无人机停在空中对三个地面目标点进行侦察。已知三个目标点在地面上的连线为直角三角形,两个点之间的最远距离为600米。问无人机与三个点同时保持500米距离时,其飞行高度为多少米?
- 3.(单选题)某学校准备重新粉刷升国旗的旗台,该旗台由两个正方体上下叠加而成,边长分别为1米和2米,问需要粉刷的面积为:
- 4.(单选题)一艘非法渔船作业时发现其正右方有海上执法船,于是沿下图所示方向左转后,立即以15节()的速度逃跑,同时执法船沿某一直线方向匀速追赶,并正好在某一点追上。已知渔船在被追上前逃跑的距离刚好与其发现执法船时
- 5.(单选题)将一个8厘米×8厘米×1厘米的白色长方体木块的外表面涂上黑色颜料,然后将其切成64个棱长1厘米的小正方体,再用这些小正方体堆成棱长4厘米的大正方体,且使黑色的面向外露的面积要尽量大,问大正方体的表面上