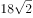试题要求
(单选题)连接正方体每个面的中心构成一个正八面体(如下图所示)。已知正方体的边长为6厘米,则正八面体的体积为多少立方厘米:


答案解析
答案:C
解析:
方法一:正八面体可以拆解成两个完全相同的四棱锥,每个棱锥的体积V=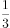 sh,高度h为正方体边长的一半,h=3厘米,棱锥的底面是下面正方体横截面(从正中间切开)里的小正方形,因此棱锥的底面积是正方体底面积的一半:6×6÷2=18平方厘米,所以每个棱锥的体积=
sh,高度h为正方体边长的一半,h=3厘米,棱锥的底面是下面正方体横截面(从正中间切开)里的小正方形,因此棱锥的底面积是正方体底面积的一半:6×6÷2=18平方厘米,所以每个棱锥的体积=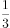 ×18×3=18立方厘米,该正八面体的体积=18×2=36立方厘米。
×18×3=18立方厘米,该正八面体的体积=18×2=36立方厘米。
方法二:该正八面体可看成由上下两个正四棱锥组成,故 ,每个四棱锥的高为立方体棱长的一半,因此可知每个四棱锥的体积=
,每个四棱锥的高为立方体棱长的一半,因此可知每个四棱锥的体积= 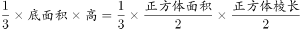 =正方体体积的
=正方体体积的 ,故该正八面体体积为正方体体积的
,故该正八面体体积为正方体体积的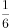 ,于是其体积=
,于是其体积=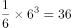 立方厘米。
立方厘米。
故正确答案为C。
方法一:正八面体可以拆解成两个完全相同的四棱锥,每个棱锥的体积V=
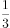 sh,高度h为正方体边长的一半,h=3厘米,棱锥的底面是下面正方体横截面(从正中间切开)里的小正方形,因此棱锥的底面积是正方体底面积的一半:6×6÷2=18平方厘米,所以每个棱锥的体积=
sh,高度h为正方体边长的一半,h=3厘米,棱锥的底面是下面正方体横截面(从正中间切开)里的小正方形,因此棱锥的底面积是正方体底面积的一半:6×6÷2=18平方厘米,所以每个棱锥的体积=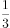 ×18×3=18立方厘米,该正八面体的体积=18×2=36立方厘米。
×18×3=18立方厘米,该正八面体的体积=18×2=36立方厘米。
方法二:该正八面体可看成由上下两个正四棱锥组成,故
 ,每个四棱锥的高为立方体棱长的一半,因此可知每个四棱锥的体积=
,每个四棱锥的高为立方体棱长的一半,因此可知每个四棱锥的体积= 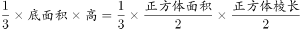 =正方体体积的
=正方体体积的 ,故该正八面体体积为正方体体积的
,故该正八面体体积为正方体体积的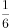 ,于是其体积=
,于是其体积=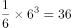 立方厘米。
立方厘米。
故正确答案为C。
考点:几何问题
相似试题
- 1.(单选题)某学校准备重新粉刷升国旗的旗台,该旗台由两个正方体上下叠加而成,边长分别为1米和2米,问需要粉刷的面积为:
- 2.(单选题)一块种植花卉的矩形土地如图所示,AD边长是AB的2倍,E是CD的中点,甲、乙、丙、丁、戊区域分别种植白花、红花、黄花、紫花、白花。则种植白花的面积占矩形土地面积的:
- 3.(单选题)草地上插了若干根旗杆,已知旗杆的高度在1至5米之间,且任意两根旗杆的距离都不超过它们高度差的10倍。如果用一根绳子将所有旗杆都围进去,在不知旗杆数量和位置的情况下,最少需要准备多少米长的绳子:
- 4.(单选题)将一块长24厘米、宽16厘米的木板分割成一个正方形和两个相同的圆形,其余部分弃去不用。在弃去不用的部分面积最小的情况下,圆的半径为多少厘米?
- 5.(单选题)某次军事演习中,一架无人机停在空中对三个地面目标点进行侦察。已知三个目标点在地面上的连线为直角三角形,两个点之间的最远距离为600米。问无人机与三个点同时保持500米距离时,其飞行高度为多少米?