试题要求
(单选题)甲、乙两人在长30米的泳池内游泳,甲每分钟游37.5米,乙每分钟游52.5米,两人同时分别从泳池的两端出发,触壁后原路返回,如是往返。如果不计转向的时间,则从出发开始计算的1分50秒内两人共相遇了多少次:
答案解析
答案:B
解析:
方法一:题目的关键在于第一次相遇,两人游过长度之和为泳池长,之后每次相遇,都需要两人再游过两个泳池长。两人一起游一个泳池长,所需时间为30÷(37.5+52.5)×60=20秒,因此两人分别在20秒时、60秒时、100秒时相遇,共相遇3次。
方法二:关键点同方法一。直接求出1分50秒两人合起来游过的距离为(37.5+52.5)×110÷60=165米,为5.5个泳池长。而两人相遇时都恰是合起来游过距离为奇数个泳池长时,也即两人分别在合游1个、3个、5个泳池长时相遇,故共相遇3次。
方法三:套用公式。先看迎面相遇, ,得
,得
 ,即有3次迎面相遇;公式:两运动体从两端同时出发,相向而行,不断往返;第N次迎面相遇,两运动体路程和=全程×
,即有3次迎面相遇;公式:两运动体从两端同时出发,相向而行,不断往返;第N次迎面相遇,两运动体路程和=全程×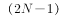 ;
;
故正确答案为B。
方法一:题目的关键在于第一次相遇,两人游过长度之和为泳池长,之后每次相遇,都需要两人再游过两个泳池长。两人一起游一个泳池长,所需时间为30÷(37.5+52.5)×60=20秒,因此两人分别在20秒时、60秒时、100秒时相遇,共相遇3次。
方法二:关键点同方法一。直接求出1分50秒两人合起来游过的距离为(37.5+52.5)×110÷60=165米,为5.5个泳池长。而两人相遇时都恰是合起来游过距离为奇数个泳池长时,也即两人分别在合游1个、3个、5个泳池长时相遇,故共相遇3次。
方法三:套用公式。先看迎面相遇,
 ,得
,得
 ,即有3次迎面相遇;公式:两运动体从两端同时出发,相向而行,不断往返;第N次迎面相遇,两运动体路程和=全程×
,即有3次迎面相遇;公式:两运动体从两端同时出发,相向而行,不断往返;第N次迎面相遇,两运动体路程和=全程×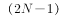 ;
;
故正确答案为B。
考点:行程问题
相似试题
- 1.(单选题)某旅游部门规划一条从甲景点到乙景点的旅游线路,经测试,旅游船从甲到乙顺水匀速行驶需3小时;从乙返回甲逆水匀速行驶需4小时,假设水流速度恒定,甲乙之间的距离为y公里,旅游船在静水中匀速行驶y公里需小时,
- 2.(单选题)一只装有动力桨的船,其单靠人工划船顺流而下的速度是水速的3倍。现该船靠人工划动从A地顺流到达B地,原路返回时只开足动力桨行驶,用时比来时少2/5。问船在静水中开足动力桨行驶的速度是人工划船速度的多少倍
- 3.(单选题)A地到B地的道路是下坡路。小周早上6:00从A地出发匀速骑车前往B地,7:00时到达两地正中间的C地。到达B地后,小周立即匀速骑车返回,在10:00时又途经C地。此后小周的速度在此前速度的基础上增加1
- 4.(单选题)A地到B地的道路是下坡路。小周早上6:00从A地出发匀速骑车前往B地,7:00时到达两地正中间的C地。到达B地后,小周立即匀速骑车返回,在10:00时又途经C地。此后小周的速度在此前速度的基础上增加1
- 5.(单选题)甲车上午8点从A地出发匀速开往B地,出发30分钟后乙车从A地出发以甲车2倍的速度前往B地,并在距离B地10千米时追上甲车。如乙车9点10分到达B地,问甲车的速度为多少千米/小时?