试题要求
(单选题)甲、乙、丙三个工程队的效率比为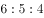 ,现将A、B两项工作量相同的工程交给这三个工程队,甲队负责A工程,乙队负责B工程,丙队参与A工程若干天后转而参与B工程。两项工程同时开工,耗时16天同时结束。
,现将A、B两项工作量相同的工程交给这三个工程队,甲队负责A工程,乙队负责B工程,丙队参与A工程若干天后转而参与B工程。两项工程同时开工,耗时16天同时结束。
问丙队在A工程中参与施工多少天:
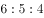 ,现将A、B两项工作量相同的工程交给这三个工程队,甲队负责A工程,乙队负责B工程,丙队参与A工程若干天后转而参与B工程。两项工程同时开工,耗时16天同时结束。
,现将A、B两项工作量相同的工程交给这三个工程队,甲队负责A工程,乙队负责B工程,丙队参与A工程若干天后转而参与B工程。两项工程同时开工,耗时16天同时结束。
问丙队在A工程中参与施工多少天:
答案解析
答案:A
解析:
方法一:根据题目给出的效率比,直接赋值三个工程队的效率分别为6、5、4,并假设丙队参与A工程y天,则根据题意可得6×16+4y=5×16+4×(16-y),解得y=6。
方法二:根据题目中的效率比,直接赋值三个工程队的效率分别为6、5、4,将两工程合在一起看成整体,则三个工程队一天的工作量为6+5+4=15,因为两项工程同时开工同时结束,则16天的总工作量为15×16=240,于是A工程的工作量为120,其中甲完成的工作量为6×16=96,则丙队需要参与A工程施工(120-96)÷4=6天。
故正确答案为A。
秒杀技:
秒杀技1:将效率比看做份数,甲比乙每天多1份,16天则多16份,而丙一天完成4份,因此完成这16份需要4天,也即丙参与A工程比参与B工程少4天,于是参与A工程的天数为(16-4)÷2=6天。
秒杀技2:由题意知,甲效率高于乙效率,因此丙必然在甲中参与天数少于16天的一半,也即答案只在A、B两项中选择,这两个选项中,优先考虑代入A项验证,符合条件。
故正确答案为A。
方法一:根据题目给出的效率比,直接赋值三个工程队的效率分别为6、5、4,并假设丙队参与A工程y天,则根据题意可得6×16+4y=5×16+4×(16-y),解得y=6。
方法二:根据题目中的效率比,直接赋值三个工程队的效率分别为6、5、4,将两工程合在一起看成整体,则三个工程队一天的工作量为6+5+4=15,因为两项工程同时开工同时结束,则16天的总工作量为15×16=240,于是A工程的工作量为120,其中甲完成的工作量为6×16=96,则丙队需要参与A工程施工(120-96)÷4=6天。
故正确答案为A。
秒杀技:
秒杀技1:将效率比看做份数,甲比乙每天多1份,16天则多16份,而丙一天完成4份,因此完成这16份需要4天,也即丙参与A工程比参与B工程少4天,于是参与A工程的天数为(16-4)÷2=6天。
秒杀技2:由题意知,甲效率高于乙效率,因此丙必然在甲中参与天数少于16天的一半,也即答案只在A、B两项中选择,这两个选项中,优先考虑代入A项验证,符合条件。
故正确答案为A。
考点:工程问题
相似试题
- 1.(单选题)某商铺甲、乙两组员工利用包装礼品的边角料制作一批花朵装饰门店。甲组单独制作需要10小时,乙组单独制作需要15小时,现两组一起做,期间乙组休息了1小时40分,完成时甲组比乙组多做300朵。问这批花有多少
- 2.(单选题)有甲、乙、丙三个工作组,已知乙组2天的工作量与甲、丙共同工作1天的工作量相同。A工程如由甲、乙组共同工作3天,再由乙、丙组共同工作7天,正好完成。如果三组共同完成,需要整7天。B工程如丙组单独完成正好
- 3.(单选题)工程队接到一项工程,投入80台挖掘机。如连续施工30天,每天工作10小时,正好按期完成。但施工过程中遭遇大暴雨,有10天时间无法施工。工期还剩8天时,工程队增派70台挖掘机并加班施工。问工程队若想按期
- 4.(单选题)某商铺甲、乙两组员工利用包装礼品的边角料制作一批花朵装饰门店。甲组单独制作需要10小时,乙组单独制作需要15小时,现两组一起做,期间乙组休息了1小时40分,完成时甲组比乙组多做300朵。问这批花有多少
- 5.(单选题)一条隧道,甲单独挖要 20 天完成,乙单独挖要 10 天完成。如果甲先挖 1 天,然后乙接替甲挖 1 天,再有甲接替乙挖 1 天……,两人如此交替工作,那么,挖完这条隧道共用多少天: