试题要求
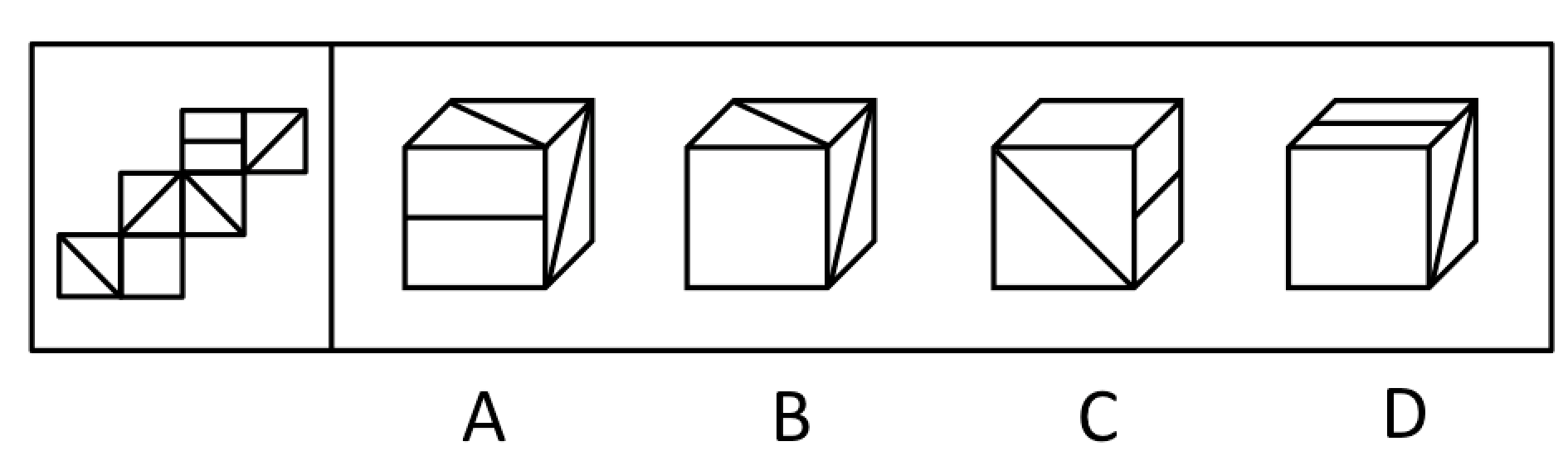
(单选题)左边给定的是纸盒的外表面,右边哪一项能由它折叠而成:

答案解析
答案:B
解析:
本题为空间重构题,首先将题干进行标号如图1所示:

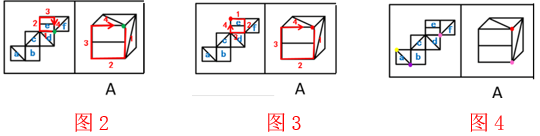
A项:横线面为e面,两个对角线面有df、cd、ac、af四种情况:
(1)假设选项为面def,那么图2中绿色点为三个面的公共点,以公共点为起点,在题干和选项中对e面沿顺时针方向进行画边,题干第一条边与e面中的横线平行,选项第一条边与横线垂直,因此不可能是面def;。
(2)题干cd面两条对角线相交于一点,选项中两条对角线并不相交,因此不可能是面ecd;。
(3)假设选项为面ace,那么图3中红色点为三个面的公共点,以公共点为起点,在题干和选项中对e面沿顺时针方向进行画边,题干第一条边与横线平行,选项第一条边与横线垂直,因此不可能是面ace。
(4)假如选项为面aef,那么三个面的交点必须和一条对角线相交,面f与面e
的交点(图4粉色点)为面def的交点,因此不能为面aef的交点,那么面aef的交点只能为面a上的紫色点或者黄色点,但是题干中,黄色点是面ac的交点,紫色点是面ab的交点,均不可能为面aef的交点,因此选项不可能是面aef。四种情况均不可能,A项错误,排除;
B项:与题干展开图一致,正确;
C项:面e与面b为相对面,不能同时出现,排除;
D项:面e与面b为相对面,不能同时出现,排除。
故正确答案为B。
本题为空间重构题,首先将题干进行标号如图1所示:


A项:横线面为e面,两个对角线面有df、cd、ac、af四种情况:
(1)假设选项为面def,那么图2中绿色点为三个面的公共点,以公共点为起点,在题干和选项中对e面沿顺时针方向进行画边,题干第一条边与e面中的横线平行,选项第一条边与横线垂直,因此不可能是面def;。
(2)题干cd面两条对角线相交于一点,选项中两条对角线并不相交,因此不可能是面ecd;。
(3)假设选项为面ace,那么图3中红色点为三个面的公共点,以公共点为起点,在题干和选项中对e面沿顺时针方向进行画边,题干第一条边与横线平行,选项第一条边与横线垂直,因此不可能是面ace。
(4)假如选项为面aef,那么三个面的交点必须和一条对角线相交,面f与面e
的交点(图4粉色点)为面def的交点,因此不能为面aef的交点,那么面aef的交点只能为面a上的紫色点或者黄色点,但是题干中,黄色点是面ac的交点,紫色点是面ab的交点,均不可能为面aef的交点,因此选项不可能是面aef。四种情况均不可能,A项错误,排除;
B项:与题干展开图一致,正确;
C项:面e与面b为相对面,不能同时出现,排除;
D项:面e与面b为相对面,不能同时出现,排除。
故正确答案为B。
考点:空间类-空间重构
相似试题
- 1.(单选题)左边给定的是纸盒的外表面,右边哪一项能由它折叠而成:
- 2.(单选题)左图给定的是正方体纸盒的外表面,下面哪一项能由它折叠而成?
- 3.(单选题)左边给定的是纸盒外表面的展开图,右边哪一项能由它折叠而成?请把它找出来:
- 4.(单选题)左边给定的是纸盒的外表面,下列哪一项能由它折叠而成?
- 5.(单选题)左边给定的是正方体的外表面展开图,下面哪一项能由它折叠而成?