试题要求
(单选题)某单位某月1—12日安排甲、乙、丙三个人值夜班,每人值班4天。三人各自值班日期数字之和相等。已知甲头两天值夜班,乙9、10日值夜班,问丙在自己第一天与最后一天值夜班之间,最多有几天不用值夜班:
答案解析
答案:D
解析:
由于连续的1-12日值班,日期数字为公差是1的等差数列,总和为 ,同时又由“三人各自值班日期数字之和相等”可知,每人的数字和为
,同时又由“三人各自值班日期数字之和相等”可知,每人的数字和为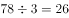 ,所以已知甲值班在1日和2日,
,所以已知甲值班在1日和2日,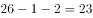 ,所以剩余的日期中11日和12日也必须是他值班;同理,乙9日和10日值班,
,所以剩余的日期中11日和12日也必须是他值班;同理,乙9日和10日值班,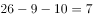 ,则3日和4日必须安排乙值班。所以剩下的5、6、7、8日就只能让丙值班,既然丙连续值班,所以他在自己第一天与最后一天值班之间没有休息日。
,则3日和4日必须安排乙值班。所以剩下的5、6、7、8日就只能让丙值班,既然丙连续值班,所以他在自己第一天与最后一天值班之间没有休息日。
故正确答案为D。
由于连续的1-12日值班,日期数字为公差是1的等差数列,总和为
 ,同时又由“三人各自值班日期数字之和相等”可知,每人的数字和为
,同时又由“三人各自值班日期数字之和相等”可知,每人的数字和为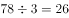 ,所以已知甲值班在1日和2日,
,所以已知甲值班在1日和2日,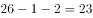 ,所以剩余的日期中11日和12日也必须是他值班;同理,乙9日和10日值班,
,所以剩余的日期中11日和12日也必须是他值班;同理,乙9日和10日值班,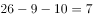 ,则3日和4日必须安排乙值班。所以剩下的5、6、7、8日就只能让丙值班,既然丙连续值班,所以他在自己第一天与最后一天值班之间没有休息日。
,则3日和4日必须安排乙值班。所以剩下的5、6、7、8日就只能让丙值班,既然丙连续值班,所以他在自己第一天与最后一天值班之间没有休息日。
故正确答案为D。
考点:其他