试题要求
(单选题)园丁将若干同样大小的花盆在平地上摆放为不同的几何图形,发现如果增加5盆,就能摆成实心正三角形。如果减少4盆,就能摆成每边多于1个花盆的实心正方形。问将现有的花盆摆成实心矩形,最外层最少有多少盆花?
答案解析
答案:D
解析:
假设组成的实心正三角形每个边有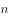 个花盆,则原有花盆数量为
个花盆,则原有花盆数量为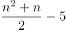 。减少4盆后,数量为
。减少4盆后,数量为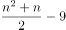 ,可组成一个实心正方形(每个边至少2个花盆),可判定其为平方数。要想最外层花的盆数少,则原有花盆数应尽可能少,即
,可组成一个实心正方形(每个边至少2个花盆),可判定其为平方数。要想最外层花的盆数少,则原有花盆数应尽可能少,即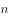 的值应尽可能小,取值验证。
的值应尽可能小,取值验证。
若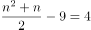 ,
,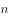 为非整数,排除;
为非整数,排除;
若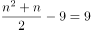 ,
,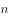 为非整数,排除;
为非整数,排除;
若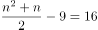 ,
,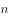 为非整数,排除;
为非整数,排除;
若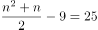 ,
,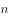 为非整数,排除;
为非整数,排除;
若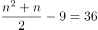 ,
,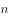 为9,满足。此时原有花盆
为9,满足。此时原有花盆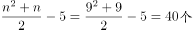 。
。
当花盆共有40个时,设实心矩形长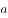 宽
宽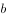 ,则
,则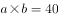 。要让最外层的花盆数最少,即长宽和
。要让最外层的花盆数最少,即长宽和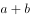 最少。根据数学知识“当
最少。根据数学知识“当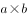 为定值时,
为定值时,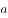 与
与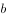 越接近,其和越小”,则当
越接近,其和越小”,则当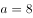 、
、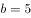 时,其长宽和最小。
时,其长宽和最小。
对最外层花盆计数时,每个端点的花盆会重复计数,故最外层的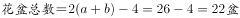 。
。
故正确答案为D。
假设组成的实心正三角形每个边有
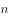 个花盆,则原有花盆数量为
个花盆,则原有花盆数量为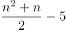 。减少4盆后,数量为
。减少4盆后,数量为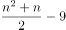 ,可组成一个实心正方形(每个边至少2个花盆),可判定其为平方数。要想最外层花的盆数少,则原有花盆数应尽可能少,即
,可组成一个实心正方形(每个边至少2个花盆),可判定其为平方数。要想最外层花的盆数少,则原有花盆数应尽可能少,即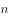 的值应尽可能小,取值验证。
的值应尽可能小,取值验证。
若
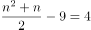 ,
,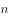 为非整数,排除;
为非整数,排除;
若
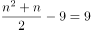 ,
,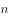 为非整数,排除;
为非整数,排除;
若
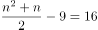 ,
,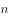 为非整数,排除;
为非整数,排除;
若
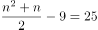 ,
,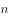 为非整数,排除;
为非整数,排除;
若
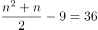 ,
,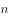 为9,满足。此时原有花盆
为9,满足。此时原有花盆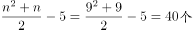 。
。
当花盆共有40个时,设实心矩形长
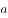 宽
宽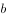 ,则
,则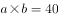 。要让最外层的花盆数最少,即长宽和
。要让最外层的花盆数最少,即长宽和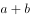 最少。根据数学知识“当
最少。根据数学知识“当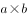 为定值时,
为定值时,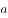 与
与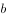 越接近,其和越小”,则当
越接近,其和越小”,则当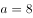 、
、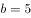 时,其长宽和最小。
时,其长宽和最小。
对最外层花盆计数时,每个端点的花盆会重复计数,故最外层的
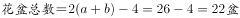 。
。
故正确答案为D。
考点:计数模型问题
相似试题
- 1.(单选题)一个面积为2平方米的长方形纸张,对折3次后得到的小长方形的面积是:
- 2.(单选题)某羽毛球赛共有23支队伍报名参赛,赛事安排23支队伍抽签两两争夺下一轮的出线权,没有抽到对手的队伍轮空,直接进入下一轮。那么,本次羽毛球赛最后共会遇到多少次轮空的情况:
- 3.(单选题)小赵,小钱,小孙一起打羽毛球,每局两人比赛 ,另一人休息,三人约定每一局的输方下一局休息,结束时算了一下,小赵休息了2局,小钱共打了8局,小孙共打了5局,则参加第9局比赛的是:
- 4.(单选题)30个人围坐在一起轮流表演节目。他们按顺序从1到3依次不重复地报数,数到3的人出来表演节目,并且表演过的人不再参加报数,那么在仅剩一个人没表演过节目的时候,共报数多少人数:
- 5.(单选题)搬运工负重徒步上楼,刚开始保持匀速,用了30秒爬了两层楼(中间不休息),之后每多爬一层多花5秒,多休息10秒,那么他爬到七楼一共用了多少秒: